QCoder

Editorial

Consider not how the bits change, but how the amplitudes change.

Let's examine the example of $n=3, a=2, L=7$ .

Let $A_i \neq 0$ be the amplitude of the basis state $\ket{i}$ , and write it from left to right. The transition of this problem can be expressed as follows.

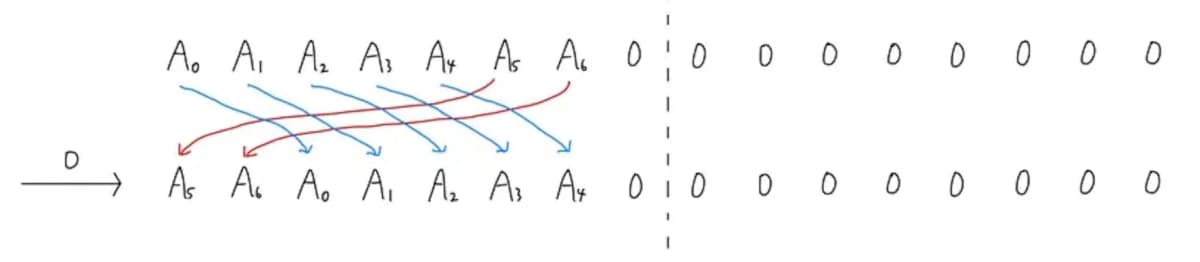
$A_{5}, A_{6}$ are moving differently from $A_{0}, A_{1}, A_{2}, A_{3}, A_{4}$ .

Here, by setting $s$ and $t$ appropriately in the operation of problem B4, the following transition can be realized.

Therefore, the operation of this problem can be realized as follows.

Note that $\mathrm{add}(a)$ represents the addition operation $\ket{x} \rightarrow \ket{(x + a) \bmod 2^{n+1}}$ , which can be implemented in the same way as B3.

The circuit depth is $O(n)$ .

Sample Code

Below is a sample program:

import math
 
from qiskit import QuantumCircuit
 
 
def qft(n: int) -> QuantumCircuit:
    qc = QuantumCircuit(n)
 
    for i in reversed(range(n)):
        qc.h(i)
        for j in reversed(range(i)):
            qc.cp(math.pi / 2 ** (i - j), j, i)
 
    for i in range(n // 2):
        qc.swap(i, n - i - 1)
 
    return qc
 
 
def crot(n: int, a: int) -> QuantumCircuit:
    qc = QuantumCircuit(n + 1)
 
    for i in range(n):
        theta = 2 * math.pi * a * 2**i / 2**n
        qc.cp(theta, n, i)
 
    return qc
 
 
def cadd(n: int, a: int) -> QuantumCircuit:
    qc = QuantumCircuit(n + 1)
 
    qc.compose(qft(n), qubits=range(n), inplace=True)
    qc.compose(crot(n, a), qubits=range(n + 1), inplace=True)
    qc.compose(qft(n).inverse(), qubits=range(n), inplace=True)
 
    return qc
 
 
# B4
def pack(n: int, s: int, t: int) -> QuantumCircuit:
    qc = QuantumCircuit(n + 1)
 
    qc.compose(cadd(n, 2 ** (n + 1) - t), qubits=range(n + 1), inplace=True)
    qc.x(n)
    qc.compose(cadd(n, -s), qubits=range(n + 1), inplace=True)
    qc.x(n)
 
    return qc
 
 
def rot(n: int, a: int) -> QuantumCircuit:
    qc = QuantumCircuit(n)
 
    for i in range(n):
        theta = 2 * math.pi * a * 2**i / 2**n
        qc.p(theta, i)
 
    return qc
 
 
def add(n: int, a: int) -> QuantumCircuit:
    qc = QuantumCircuit(n)
 
    qc.compose(qft(n), qubits=range(n), inplace=True)
    qc.compose(rot(n, a), qubits=range(n), inplace=True)
    qc.compose(qft(n).inverse(), qubits=range(n), inplace=True)
 
    return qc
 
 
def solve(n: int, a: int, L: int) -> QuantumCircuit:
    qc = QuantumCircuit(n + 1)
 
    qc.compose(add(n + 1, 2**n - L + a), qubits=range(n + 1), inplace=True)
    qc.compose(pack(n, 2**n - L + a, 2**n + a), qubits=range(n + 1), inplace=True)
    qc.compose(add(n + 1, a), qubits=range(n + 1), inplace=True)
 
    return qc

B5: Modular Arithmetic I

Editorial

Sample Code