A5: Minus One Oracle

Editorial

First, let's consider an operation $\ket{x} \rightarrow \ket{(x - 1) \bmod {2^n}}$ that is the inverse of $\ket{x} \rightarrow \ket{(x + 1) \bmod {2^n}}$.

Let $x$ be represented by a bit string $x_0x_1 \cdots x_{n-1}$.

Based on this representation, the operation $\ket{x} \rightarrow \ket{(x + 1) \bmod {2^n}}$ can be rephrased as follows:

• Convert all consecutive $1$'s from the least significant bit to $0$ and flip the first $0$ bit to $1$.
  • Specifically, find $i$ $(1 \leq i < n)$ such that "$x_0 = x_1 = \cdots = x_{i-1} = 1, x_{i} = 0$" and flip $x_0, x_1, \cdots , x_{i-1}$ to $0$ and $x_i$ to $1$. If "$x_0 = x_1 = \cdots = x_{n-1} = 1$", flip $x_0, x_1, \cdots , x_{n-1}$ to $0$. If "$x_0 = x_1 = \cdots = x_{n-1} = 0$", flip $x_0$ to $1$.

Let's consider the example of $n = 3$ below.

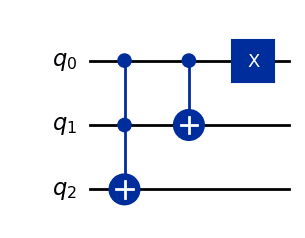
Assume that the input state is $\ket{110}$.

First, the state transition is as follows by the "multi-controlled $X$ gate¹" with the first and second qubits as control bits and the third qubit as the target bit.

Next, the state transition is as follows by the "controlled $X$ gate with the first qubit as the control bit and the second qubit as the target bit".

Finally, the state transition is as follows by the $X$ gate.

As a result, the operation $\ket{110} \rightarrow \ket{001}$ is realized.

By generalizing the above operation, the operation $\ket{x} \rightarrow \ket{(x + 1) \bmod {2^n}}$ can be realized, and the code is as follows:

from qiskit import QuantumCircuit
 
 
def solve(n: int) -> QuantumCircuit:
    qc = QuantumCircuit(n)
 
    for i in reversed(range(1, n)):
        qc.mcx(list(range(i)), i)
 
    qc.x(0)
 
    return qc

By applying these gates in reverse order, the operation $\ket{x} \rightarrow \ket{(x - 1) \bmod {2^n}}$ is realized.

Sample Code

Below is a sample program:

from qiskit import QuantumCircuit
 
 
def solve(n: int) -> QuantumCircuit:
    qc = QuantumCircuit(n)
 
    qc.x(0)
 
    for i in range(1, n):
        qc.mcx(list(range(i)), i)
 
    return qc

Equivalently, you can use the inverse method.

from qiskit import QuantumCircuit
 
 
def solve(n: int) -> QuantumCircuit:
    qc = QuantumCircuit(n)
 
    for i in reversed(range(1, n)):
        qc.mcx(list(range(i)), i)
 
    qc.x(0)
 
    return qc.inverse()

Follow-up

By decomposing a positive integer $a$ into the sum of $2^0, 2^1, \ldots$ and $2^n-2^0, 2^{n}-2^1, \ldots$, the algorithm of this problem can realize $\ket{x} \rightarrow \ket{x + a \pmod {2^n}}$ by applying the algorithm at most $\left\lceil \frac{\log_2(a) + 1}{2}\right\rceil$ times.