A3: Cyclic Shift Oracle I

Editorial

You can solve this problem by using the swap gate implemented in problem A2.

Let's consider the following example of $3$ qubits:

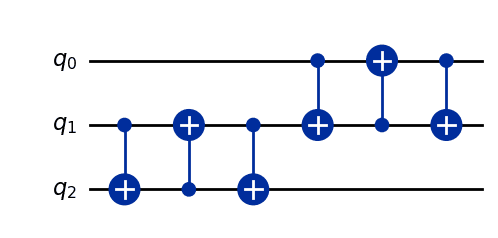
First, swap the second and third qubits.

Next, swap the first and second qubits.

As a result, the quantum state $\ket{x_2x_0x_1}$ can be obtained by two swaps.

By generalizing the above operation, the quantum state $\ket{x_{n-1}x_0x_1\cdots x_{n-2}}$ can be generated by $n-1$ swaps. Since each swap can be implemented with a depth $3$ quantum circuit, the depth of the entire quantum circuit is $3(n-1)$, allowing you to solve this problem.

Sample Code

Below is a sample program:

from qiskit import QuantumCircuit
 
 
def solve(n: int) -> QuantumCircuit:
    def swap(n: int, qubit1: int, qubit2: int) -> QuantumCircuit:
        qc = QuantumCircuit(n)
 
        qc.cx(qubit1, qubit2)
        qc.cx(qubit2, qubit1)
        qc.cx(qubit1, qubit2)
 
        return qc
 
    qc = QuantumCircuit(n)
 
    for i in reversed(range(n - 1)):
        qc.compose(swap(n, i, i + 1), inplace=True)
 
    return qc

Follow-up

After the contest, a solution with a circuit depth of $3 \lceil \log_2 n \rceil$ was discovered by hiryuN (tweet). This algorithm is derived by reinterpreting the algorithm for A4: Cyclic Shift Oracle, which transforms $\ket{x}\rightarrow \ket{(x+1) \bmod n}$, as an operation that replaces the $i$-th bit with the $(i+1) \bmod n$-th bit.