LogoQCoder Programming Contest 003
Sign in
← Previous ProblemNext Problem →

B6: Grover's Algorithm I

Time Limit: 3 sec

Memory Limit: 512 MiB

Score: 300

Writer: Not_Leonian

Editorial

This problem is about amplifying the probability amplitude of a specific computational basis state and assumes the use of Grover's algorithm.

Let us defined the quantum state ∣ψ⟩\ket{\psi} by

∣ψ⟩=12n∑i=02n−1∣i⟩.\begin{equation} \ket{\psi} = \frac{1}{\sqrt{2^n}} \sum_{i=0}^{2^n-1} \ket{i} \end{equation}.

Grover's algorithm consists of the following steps:

  1. Prepare the quantum state ∣ψ⟩\ket{\psi}.
  2. Repeat the next operation called Grover iteration:
    1. Apply an operation that flips the sign of only the computational basis state to be amplified.
    2. Apply the operator represented by 2∣ψ⟩⟨ψ∣−I2 \ket{\psi}\bra{\psi} - I.

By applying the HH gates to all qubits, we can prepare the quantum state ∣ψ⟩\ket{\psi}. In this problem, the operation that flips the sign of only the computational basis state to be amplified is the oracle OO itself. The operation represented by the operator 2∣ψ⟩⟨ψ∣−In2 \ket{\psi}\bra{\psi} - I_n is the one implemented in B5.

Considering the above, let's calculate the quantum state after performing one Grover iteration.

First, regarding the inner product between the quantum state ∣ψ⟩\ket{\psi} and ∣L⟩\ket{L}:

⟨ψ∣L⟩=⟨L∣ψ⟩=1/2n\begin{equation} \braket{\psi|L}=\braket{L|\psi}=1/\sqrt{2^n} \end{equation}

Noting that the oracle OO can be expressed as I−2∣L⟩⟨L∣I-2\ket{L}\bra{L}, we see that applying the oracle OO to ∣ψ⟩\ket{\psi} gives:

O∣ψ⟩=(I−2∣L⟩⟨L∣)∣ψ⟩=∣ψ⟩−2∣L⟩⟨L∣ψ⟩=∣ψ⟩−22n∣L⟩\begin{equation} O \ket{\psi} = (I - 2\ket{L}\bra{L}) \ket{\psi} = \ket{\psi} - 2\ket{L} \braket{L|\psi} = \ket{\psi} - \frac{2}{\sqrt{2^n}} \ket{L} \end{equation}

Next, by applying the operator expressed as 2∣ψ⟩⟨ψ∣−In2 \ket{\psi}\bra{\psi} - I_n, we get:

(2∣ψ⟩⟨ψ∣−I)(∣ψ⟩−22n∣L⟩)=2∣ψ⟩⟨ψ∣ψ⟩−∣ψ⟩−42n∣ψ⟩⟨ψ∣L⟩+22n∣L⟩=2∣ψ⟩−∣ψ⟩−42n∣ψ⟩+22n∣L⟩=2n−42n∣ψ⟩+22n∣L⟩\begin{align} (2 \ket{\psi}\bra{\psi} - I) (\ket{\psi} - \frac{2}{\sqrt{2^n}} \ket{L}) &= 2 \ket{\psi} \braket{\psi|\psi} - \ket{\psi} - \frac{4}{\sqrt{2^n}} \ket{\psi} \braket{\psi|L}+\frac{2} {\sqrt{2^n}} \ket{L} \\ &= 2 \ket{\psi} - \ket{\psi} - \frac{4}{2^n} \ket{\psi} + \frac{2}{\sqrt{2^n}} \ket{L} \\ &= \frac{2^n-4}{2^n} \ket{\psi} + \frac{2}{\sqrt{2^n}} \ket{L} \end{align}

The value of aLa_L after performing the operation is given by:

aL=2n−42n2n+22n\begin{equation} a_L=\frac{2^n-4}{2^n\sqrt{2^n}}+\frac{2}{\sqrt{2^n}} \end{equation}

Therefore, under the constraint of n≥3n \geq 3, it holds that ∣aL∣2>4/2n|a_L|^2 > 4/2^n. Thus, by performing Grover's algorithm for one iteration, we can solve this problem.

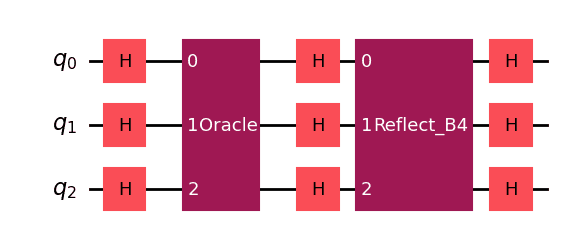
For the case where n=3n = 3, the circuit diagram is shown below. The Reflect_B4 in the circuit diagram indicates the circuit of problem B4.

Sample Code

Below is a sample program:

from qiskit import QuantumCircuit
from qiskit.circuit.library import ZGate
 
 
def reflect(n: int) -> QuantumCircuit:
    qc = QuantumCircuit(n)
 
    qc.x(range(n))
    qc.append(ZGate().control(n - 1), range(n))
    qc.x(range(n))
 
    return qc
 
 
def solve(n: int, o: QuantumCircuit) -> QuantumCircuit:
    qc = QuantumCircuit(n)
 
    qc.h(range(n))
    qc.compose(o, inplace=True)
    qc.h(range(n))
    qc.compose(reflect(n), inplace=True)
    qc.h(range(n))
 
    return qc