LogoQCoder Programming Contest 003
Sign in
← Previous ProblemNext Problem →

B5: Reflection Operator II

Time Limit: 3 sec

Memory Limit: 512 MiB

Score: 200

Writer: Not_Leonian

Editorial

When applying the HH gates to all qubits, the zero state ∣0⟩\ket{0} transitions to ∣ψ⟩\ket{\psi}. In other words, ∣ψ⟩\ket{\psi} can be expressed as

∣ψ⟩=H⊗n∣0⟩.\begin{equation} \ket{\psi} = H^{\otimes n} \ket{0}. \end{equation}

Due to the properties of the HH gate, we have

H⊗n=(H⊗n)†, (H⊗n)2=I.\begin{equation} H^{\otimes n}=(H^{\otimes n})^{\dagger},\ (H^{\otimes n})^2=I. \end{equation}

Using the properties of adjoint matrices, we can also derive

⟨ψ∣=∣ψ⟩†=(H⊗n∣0⟩)†=∣0⟩†(H⊗n)†=⟨0∣H⊗n.\begin{equation} \bra{\psi} = \ket{\psi}^{\dagger} = (H^{\otimes n} \ket{0})^{\dagger} = \ket{0}^{\dagger}(H^{\otimes n})^{\dagger} = \bra{0} H^{\otimes n}. \end{equation}

This allows us to transform 2∣ψ⟩⟨ψ∣−I2 \ket{\psi}\bra{\psi} - I as follows:

2∣ψ⟩⟨ψ∣−I=2H⊗n∣0⟩⟨0∣H⊗n−(H⊗n)2=H⊗n(2∣0⟩⟨0∣−I)H⊗n\begin{equation} 2 \ket{\psi}\bra{\psi} - I = 2 H^{\otimes n} \ket{0}\bra{0} H^{\otimes n} - (H^{\otimes n})^2 = H^{\otimes n} (2 \ket{0}\bra{0} - I) H^{\otimes n} \end{equation}

Therefore, by applying the HH gates to all qubits, implementing the circuit of problem B4, and applying the HH gate to all qubits again, we can solve this problem.

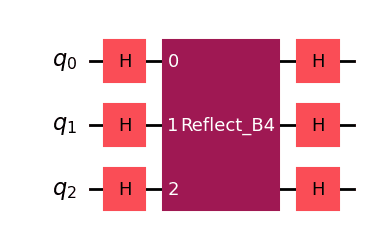
For the case where n=3n = 3, the circuit diagram is shown below. The Reflect_B4 in the circuit diagram indicates the circuit of problem B4.

Sample Code

Below is a sample program:

from qiskit import QuantumCircuit
from qiskit.circuit.library import ZGate
 
 
def reflect(n: int) -> QuantumCircuit:
    qc = QuantumCircuit(n)
 
    qc.x(range(n))
    qc.append(ZGate().control(n - 1), range(n))
    qc.x(range(n))
 
    return qc
 
 
def solve(n: int) -> QuantumCircuit:
    qc = QuantumCircuit(n)
 
    qc.h(range(n))
    qc.compose(reflect(n), inplace=True)
    qc.h(range(n))
 
    return qc