B2: Phase Shift Oracle

Editorial

This problem involves implementing a quantum circuit that applies a phase shift gate $P(\theta)$ exclusively to a specific computational basis state $\ket{L}$.

So, how can we apply the phase shift gate $P(\theta)$ only to the specific computational basis state $\ket{L}$within a superposition?

This can be achieved with the following steps:

1. For $\ket{L} = \ket{L_0 L_1 L_2 ... L_{n-1}}$, apply the $X$ gate at index $i$ where $L_i = 0$. This transforms $\ket{L}$ into $\ket{2^n - 1} = \ket{1...1}$.
2. Apply a multiple-control phase shift gate, using $n - 1$ bits as control bits and the remaining $1$ bit as the target bit. In this case, the phase shift gate acts only on the computational basis state $\ket{L}$ within the superposition.
3. Perform the inverse of step 1 to transform $\ket{2^n - 1}$ back to $\ket{L}$.

The circuit diagram for the case where $n = 3$ and $L = 1$ is shown as follows.

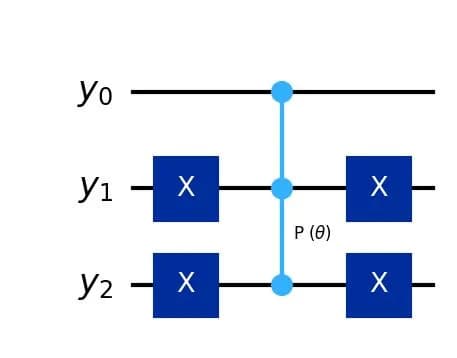
The circuit depth is $3$.

Sample Code

Below is a sample program:

from qiskit import QuantumCircuit
 
 
def solve(n: int, L: int, theta: float) -> QuantumCircuit:
    qc = QuantumCircuit(n)
 
    for i in range(n):
        if not (1 << i) & L:
            qc.x(i)
 
    if n == 1:
        qc.p(theta, n - 1)
    else:
        qc.mcp(theta, list(range(n - 1)), n - 1)
 
    for i in range(n):
        if not (1 << i) & L:
            qc.x(i)
 
    return qc