LogoQCoder Programming Contest 002
Sign in
← Previous ProblemNext Problem →

B1: Generate State eiθ∣0⟩e^{i\theta}\ket{0}

Time Limit: 3 sec

Memory Limit: 512 MiB

Score: 100

Writer: PSL

Editorial

In this problem, you can transition from the zero state ∣0⟩\ket{0} to the state eiθ∣0⟩e^{i\theta}\ket{0} using the XX and phase shift (P(θ)P(\theta)) gates.

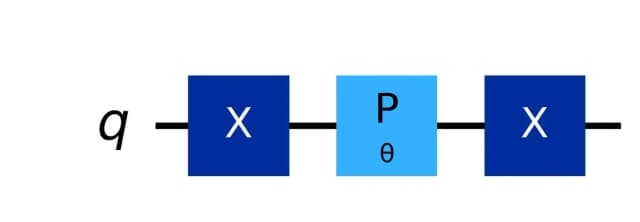
First, apply the XX gate to the quantum state ∣0⟩\ket{0} to transition it to the quantum state ∣1⟩\ket{1}.

∣0⟩→X(0)∣1⟩\begin{equation} \ket{0} \xrightarrow{X(0)} \ket{1} \end{equation}

Next, apply the phase shift gate to the quantum state ∣1⟩\ket{1} to transition it to the quantum state eiθ∣1⟩e^{i\theta}\ket{1}.

∣1⟩→P(θ,0)eiθ∣1⟩\begin{equation} \ket{1} \xrightarrow{P(\theta, 0)} e^{i\theta}\ket{1} \end{equation}

Finally, apply the XX gate to the quantum state eiθ∣1⟩e^{i\theta}\ket{1} to transition it to the quantum state eiθ∣0⟩e^{i\theta}\ket{0}.

eiθ∣1⟩→X(0)eiθ∣0⟩\begin{equation} e^{i\theta}\ket{1}\xrightarrow{X(0)} e^{i\theta}\ket{0} \end{equation}

eiπ∣0⟩=−∣0⟩e^{i\pi}\ket{0} = -\ket{0} suggests that this problem can be considered a generalization of Problem A1 (Generate State −∣0⟩-\ket{0}).

Sample Code

Below is a sample program:

from qiskit import QuantumCircuit
 
 
def solve(theta: float) -> QuantumCircuit:
    qc = QuantumCircuit(1)
 
    qc.x(0)
    qc.p(theta, 0)
    qc.x(0)
 
    return qc