LogoQCoder Programming Contest 003
Sign in
← Previous ProblemNext Problem →

Ex1: Convert Bit-Flip into Phase-Flip II

Time Limit: 3 sec

Memory Limit: 512 MiB

Score: 300

Writer: Not_Leonian

Editorial

When an XX gate and an HH gate are applied sequentially to the rightmost qubit, it results in the following:

∣x⟩n∣0⟩1→X∣x⟩n∣1⟩1→H12(∣x⟩n∣0⟩1−∣x⟩n∣1⟩1)\begin{equation} \ket{x}_n\ket{0}_1 \xrightarrow{X} \ket{x}_n\ket{1}_1 \xrightarrow{H} \frac{1}{\sqrt{2}} (\ket{x}_n\ket{0}_1 - \ket{x}_n\ket{1}_1) \end{equation}

By applying the oracle OO, it results in the following:

12(∣x⟩n∣0⟩1−∣x⟩n∣1⟩1)→O{12(∣x⟩n∣1⟩1−∣x⟩n∣0⟩1)(f(x)=1)12(∣x⟩n∣0⟩1−∣x⟩n∣1⟩1)(f(x)=0)\begin{equation} \frac{1}{\sqrt{2}} (\ket{x}_n\ket{0}_1 - \ket{x}_n\ket{1}_1) \xrightarrow{O} \begin{cases} \frac{1}{\sqrt{2}} (\ket{x}_n\ket{1}_1 - \ket{x}_n\ket{0}_1) & (f(x)=1) \\ \frac{1}{\sqrt{2}} (\ket{x}_n\ket{0}_1 - \ket{x}_n\ket{1}_1) & (f(x)=0) \end{cases} \end{equation}

By noting that 12(∣x⟩n∣1⟩1−∣x⟩n∣0⟩1)=−12(∣x⟩n∣0⟩1−∣x⟩n∣1⟩1)\frac{1}{\sqrt{2}} (\ket{x}_n\ket{1}_1 - \ket{x}_n\ket{0}_1) = - \frac{1}{\sqrt{2}} (\ket{x}_n\ket{0}_1 - \ket{x}_n\ket{1}_1), and applying an HH gate and then an XX gate in sequence to the rightmost qubit, we obtain the following, which indicates that the expected operation has been implemented:

{12(∣x⟩n∣1⟩1−∣x⟩n∣0⟩1)(f(x)=1)12(∣x⟩n∣0⟩1−∣x⟩n∣1⟩1)(f(x)=0)→H{−∣x⟩n∣1⟩1(f(x)=1)∣x⟩n∣1⟩1(f(x)=0)→X{−∣x⟩n∣0⟩1(f(x)=1)∣x⟩n∣0⟩1(f(x)=0)\begin{align} \begin{cases} \frac{1}{\sqrt{2}} (\ket{x}_n\ket{1}_1 - \ket{x}_n\ket{0}_1) & (f(x)=1) \\ \frac{1}{\sqrt{2}} (\ket{x}_n\ket{0}_1 - \ket{x}_n\ket{1}_1) & (f(x)=0) \end{cases} & \xrightarrow{H} \begin{cases} -\ket{x}_n\ket{1}_1 & (f(x)=1) \\ \ket{x}_n\ket{1}_1 & (f(x)=0) \end{cases} \\ & \xrightarrow{X} \begin{cases}-\ket{x}_n\ket{0}_1 & (f(x)=1) \\ \ket{x}_n\ket{0}_1 & (f(x)=0) \end{cases} \end{align}

For the case where n=3n = 3, the circuit diagram is shown below.

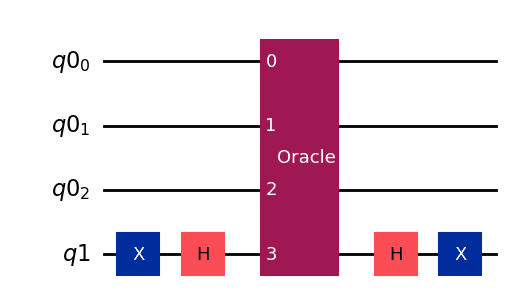
Sample Code

Below is a sample program:

from qiskit import QuantumCircuit, QuantumRegister
 
 
def solve(n: int, o: QuantumCircuit) -> QuantumCircuit:
    x, y = QuantumRegister(n), QuantumRegister(1)
    qc = QuantumCircuit(x, y)
 
    qc.x(y)
    qc.h(y)
    qc.compose(o, inplace=True)
    qc.h(y)
    qc.x(y)
 
    return qc