A5: Generate One-hot Superposition State II

Editorial

In the intended solution for problem A4, the depth of the quantum circuit would be $2n - 1$, which does not solve this problem. So, how can we improve the quantum circuit?

Let's examine the following example with 4 qubits:

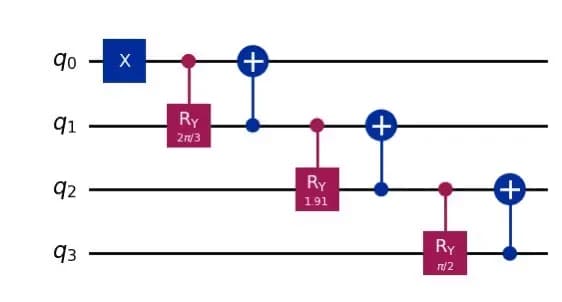
This quantum circuit generates the quantum state $\frac{1}{\sqrt{4}} (\ket{1000} + \ket{0100} + \ket{0010} + \ket{0001})$. Each quantum gate acts only after all the previous gates have acted, and they cannot act simultaneously.

In this circuit, a controlled $R_y$ gate and a controlled $X$ gate are applied consecutively to the same qubit. We should instead consider applying all controlled $R_y$ gates first, followed by the controlled $X$ gates.

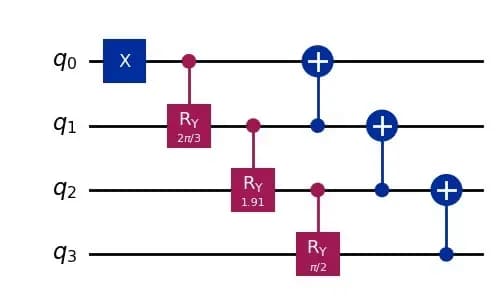
By doing this, the last controlled $R_y$ gate and the first controlled $X$ gate act on different pairs of qubits, allowing them to act simultaneously. As a result, the depth of the quantum circuit improved from 7 to 6.

By generalizing these operation to arbitrary $n$ qubits, the depth of the quantum circuit becomes $n + 2$, which satisfies the given constraint.

Sample Code

Below is a sample program:

import math
 
from qiskit import QuantumCircuit
 
 
def solve(n: int) -> QuantumCircuit:
    qc = QuantumCircuit(n)
 
    theta = [2 * math.atan(math.sqrt(i)) for i in range(n - 1, 0, -1)]
 
    qc.x(0)
 
    for i in range(n - 1):
        qc.cry(theta[i], i, i + 1)
 
    for i in range(n - 1):
        qc.cx(i + 1, i)
 
    return qc