LogoQCoder Programming Contest 002
Sign in
← Previous ProblemNext Problem →

B7: Quantum Arithmetic III

Time Limit: 3 sec

Memory Limit: 512 MiB

Score: 200

Writer: PSL

Editorial

This problem can be solved by replacing the initial Hadamard gates in the solution for Problem B6 with a quantum Fourier transform.

The circuit diagram for the case where n=2n = 2 and m=2m = 2 is shown as follows.

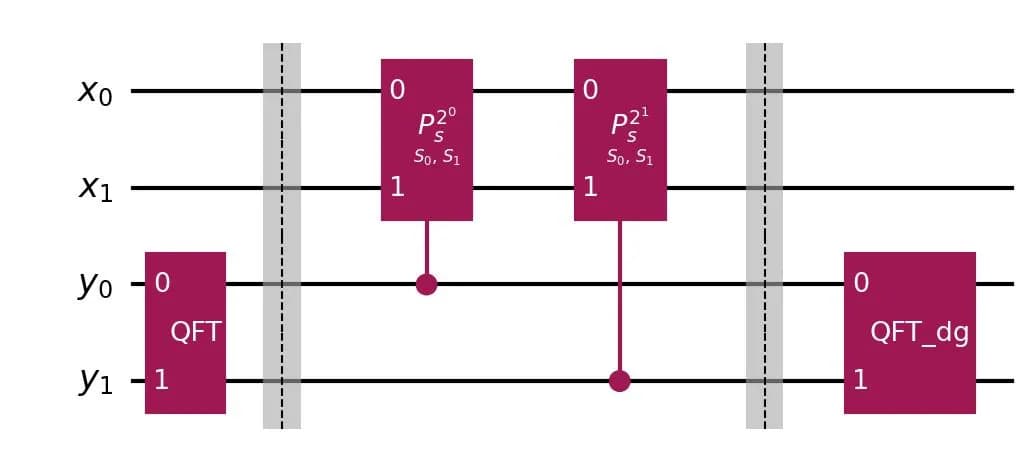
Let's examine the state transitions of the computational basis state ∣x⟩n∣y⟩m\ket{x}_n \ket{y}_m.

First, we apply the quantum Fourier transform to the register ∣y⟩m\ket{y}_m.

∣y⟩m→QFT12m∑k=02m−1exp⁡(2πiyk2m)∣k⟩m\begin{equation} \ket{y}_m \xrightarrow{\mathrm{QFT}} \sqrt{\frac{1}{2^m}} \sum_{k=0}^{2^m-1} \exp{\left(\frac{2\pi i y k}{2^m}\right)} \ket{k}_m \end{equation}

Next, we apply the oracles PS2jP_{S}^{2^j} defined in the editorial for Problem B6 using the jj-th qubit of the register ∣y⟩m\ket{y}_m as the control qubit.

12m∑k=02m−1exp⁡(2πiyk2m)∣k⟩m→PS20,PS21,⋯ ,PS2m−112m∑k=02m−1e2πi(y+f(x))k2m∣k⟩m\begin{equation} \sqrt{\frac{1}{2^m}} \sum_{k=0}^{2^m-1} \exp{\left(\frac{2\pi i y k}{2^m}\right)} \ket{k}_m \xrightarrow{P_S^{2^0}, P_S^{2^1}, \cdots, P_S^{2^{m-1}}} \frac{1}{\sqrt{2^m}} \sum_{k=0}^{2^m-1} e^{\frac{2\pi i (y + f(x))k}{2^m}} \ket{k}_m \end{equation}

Finally, by applying the inverse quantum Fourier transform, we can transition the register ∣y⟩m\ket{y}_m to the desired state.

12m∑k=02m−1e2πi(y+f(x))k2m∣k⟩m→IQFT∣(y+f(x)) mod 2m⟩m\begin{align} \frac{1}{\sqrt{2^m}} \sum_{k=0}^{2^m-1} e^{\frac{2\pi i (y + f(x))k}{2^m}} \ket{k}_m \xrightarrow{\mathrm{IQFT}} \ket{(y + f(x))\ \mathrm{mod}\ 2^m}_m \end{align}

Through these operations, we can implement a quantum circuit that realizes the state transition expressed as

∣x⟩n∣0⟩m→qc∣x⟩n∣(y+f(x)) mod 2m⟩m.\begin{equation} \ket{x}_{n}\ket{0}_{m} \xrightarrow{\mathrm{qc}} \ket{x}_{n}\ket{(y + f(x))\ \mathrm{mod}\ 2^m}_m. \end{equation}

The circuit depth is 4m+max(n,m)4m + \mathrm{max}(n, m).

Sample Code

Below is a sample program:

import math
 
from qiskit import QuantumCircuit, QuantumRegister
 
 
def qft(n: int) -> QuantumCircuit:
    qc = QuantumCircuit(n)
 
    for i in reversed(range(n)):
        qc.h(i)
        for j in reversed(range(i)):
            qc.cp(math.pi / 2 ** (i - j), j, i)
 
    for i in range(n // 2):
        qc.swap(i, n - i - 1)
 
    return qc
 
 
def solve(n: int, m: int, S: list[int]) -> QuantumCircuit:
    x, y = QuantumRegister(n), QuantumRegister(m)
    qc = QuantumCircuit(x, y)
    qft_m = qft(m)
 
    qc.compose(qft_m, y, inplace=True)
 
    for j in range(m):
        for i in range(n):
            theta = (2 * math.pi * S[i] / 2**m) * 2**j
            qc.cp(theta, x[i], y[j])
 
    qc.compose(qft_m.inverse(), y, inplace=True)
 
    return qc