LogoQCoder Programming Contest 002
Sign in
← Previous ProblemNext Problem →

B5: Quantum Arithmetic I

Time Limit: 3 sec

Memory Limit: 512 MiB

Score: 200

Writer: PSL

Editorial

In this problem, you will implement an oracle OO that performs the state transition expressed as

∣x⟩n→Oexp⁡(2πif(x)2m)∣x⟩n.\begin{equation} \ket{x}_n \xrightarrow{O} \exp{\left(\frac{2\pi i f(x)}{2^m}\right)}\ket{x}_n. \end{equation}

Here, the resulting state after the transition can be decomposed independently for each qubit as follows:

exp⁡(2πif(x)2m)∣x⟩n=exp⁡(2πi(S0x0+⋯+Sn−1xn−1)2m)∣x0⋯xn−1⟩=exp⁡(2πiS0x02m)∣x0⟩⊗exp⁡(2πiS1x12m)∣x1⟩⊗⋯⊗exp⁡(2πiSn−1xn−12m)∣xn−1⟩\begin{align} \exp{\left(\frac{2\pi i f(x)}{2^m}\right)}\ket{x}_n &= \exp{\left(\frac{2\pi i ( S_0 x_0 + \cdots + S_{n-1}x_{n-1})}{2^m}\right)} \ket{x_0 \cdots x_{n-1}} \nonumber\\ &= \exp{\left(\frac{2\pi i S_0 x_0}{2^m}\right)} \ket{x_0} \otimes \exp{\left(\frac{2\pi i S_1 x_1}{2^m}\right)} \ket{x_1} \otimes \cdots \otimes \exp{\left(\frac{2\pi i S_{n-1} x_{n-1}}{2^m}\right)} \ket{x_{n-1}} \end{align}

Thus, by applying a phase shift gate with a phase of θ=2πSi/2m\theta = 2\pi S_i / 2^m to each qubit xix_i, you can solve this problem.

The circuit diagram for the case where n=3n = 3 is shown as follows.

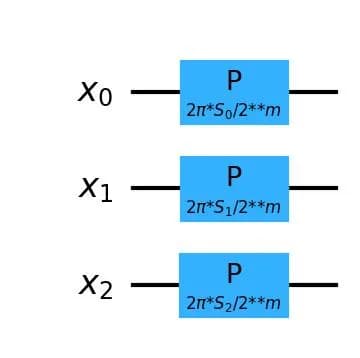
The circuit depth is 11.

Sample Code

Below is a sample program:

import math
 
from qiskit import QuantumCircuit
 
 
def solve(n: int, m: int, S: list[int]) -> QuantumCircuit:
    qc = QuantumCircuit(n)
 
    for i in range(n):
        theta = 2 * math.pi * S[i] / 2**m
        qc.p(theta, i)
 
    return qc