LogoQCoder Programming Contest 002
Sign in
Next Problem →

A1: Generate State −∣0⟩- \ket{0}

Time Limit: 3 sec

Memory Limit: 512 MiB

Score: 100

Writer: ST12

Editorial

Quantum computers use the concept of "quantum gates" to manipulate the state of qubits.

In this problem, you can transition from the zero state ∣0⟩\ket{0} to the state -∣0⟩\ket{0} using the XX and ZZ gates.

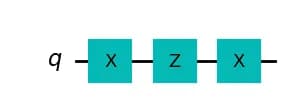
First, apply the XX gate to the quantum state ∣0⟩\ket{0} to transition it to the quantum state ∣1⟩\ket{1}.

∣0⟩→X(0)∣1⟩\begin{equation} \ket{0} \xrightarrow{X(0)} \ket{1} \end{equation}

Next, apply the ZZ gate to the quantum state ∣1⟩\ket{1} to transition it to the quantum state −∣1⟩-\ket{1}.

∣1⟩→Z(0)−∣1⟩\begin{equation} \ket{1} \xrightarrow{Z(0)} - \ket{1} \end{equation}

Finally, apply the XX gate to the quantum state −∣1⟩-\ket{1} to transition it to the quantum state −∣0⟩-\ket{0}.

−∣1⟩→X(0)−∣0⟩\begin{equation} - \ket{1} \xrightarrow{X(0)} - \ket{0} \end{equation}

Although the global phase of ∣0⟩\ket{0} changes from 00 to π\pi, when measuring this qubit, the original state ∣0⟩\ket{0} is observed with a probability of 1.

These bit flips and phase flips are fundamental quantum operations.

Sample Code

Below is a sample program:

from qiskit import QuantumCircuit
 
 
def solve() -> QuantumCircuit:
    qc = QuantumCircuit(1)
    
    # Apply PauliX gate and PauliZ gate to the 1st qubit (index 0)
    qc.x(0)
    qc.z(0)
    qc.x(0)
 
    return qc

Supplementary Information