QCoder

解説

この問題は特定の計算基底状態の確率振幅を増幅する問題であり、グローバーのアルゴリズムの使用を想定しています。

量子状態 $\ket{\psi}$ を次式で定義します。

\begin{equation} \ket{\psi} = \frac{1}{\sqrt{2^n}} \sum_{i=0}^{2^n-1} \ket{i} \end{equation}

グローバーのアルゴリズムとは以下のようなアルゴリズムです。

量子状態 $\ket{\psi}$ を用意する。
Grover iterationと呼ばれる次の操作を繰り返す。
1. 増幅したい計算基底状態のみの符号を反転させる操作を適用する。
2. 演算子 $2 \ket{\psi}\bra{\psi} - I$ で表される操作を適用する。

全ての量子ビットに $H$ ゲートを作用させることで、量子状態 $\ket{\psi}$ を用意できます。また、この問題において、増幅したい計算基底状態のみの符号を反転させる操作はオラクル $O$ そのものです。そして、演算子 $2 \ket{\psi}\bra{\psi} - I$ で表される操作は、B5で実装した操作です。

上記を踏まえて、Grover iterationを $1$ 回のみ行った場合の量子状態を計算してみましょう。

まず、量子状態 $\ket{\psi}$ と $\ket{L}$ の内積について

\begin{equation} \braket{\psi|L}=\braket{L|\psi}=1/\sqrt{2^n} \end{equation}

が成立するため、オラクル $O$ が $I-2\ket{L}\bra{L}$ と表せることに注目し、 $\ket{\psi}$ にオラクル $O$ を作用させると、以下のようになります。

\begin{equation} O \ket{\psi} = (I - 2\ket{L}\bra{L}) \ket{\psi} = \ket{\psi} - 2\ket{L} \braket{L|\psi} = \ket{\psi} - \frac{2}{\sqrt{2^n}} \ket{L} \end{equation}

次に、 $2 \ket{\psi}\bra{\psi} - I$ と表現される演算子を作用させると、以下のようになります。

\begin{align} (2 \ket{\psi}\bra{\psi} - I) (\ket{\psi} - \frac{2}{\sqrt{2^n}} \ket{L}) &= 2 \ket{\psi} \braket{\psi|\psi} - \ket{\psi} - \frac{4}{\sqrt{2^n}} \ket{\psi} \braket{\psi|L}+\frac{2} {\sqrt{2^n}} \ket{L} \\ &= 2 \ket{\psi} - \ket{\psi} - \frac{4}{2^n} \ket{\psi} + \frac{2}{\sqrt{2^n}} \ket{L} \\ &= \frac{2^n-4}{2^n} \ket{\psi} + \frac{2}{\sqrt{2^n}} \ket{L} \end{align}

操作を行った後の $a_L$ は以下のようになります。

\begin{equation} a_L=\frac{2^n-4}{2^n\sqrt{2^n}}+\frac{2}{\sqrt{2^n}} \end{equation}

したがって、制約の $n\geq 3$ のもとで、 $|a_L|^2\gt 4/2^n$ が成立します。よって、Grover iterationの回数を $1$ 回としてグローバーのアルゴリズムを行えば、この問題を解くことができます。

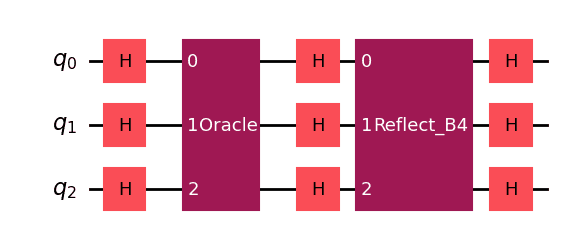
$n = 3$ の場合の回路図は、以下の通りです。回路図内のReflect_B4は、B4の回路を示しています。

解答例

解答例は以下の通りです。

from qiskit import QuantumCircuit
from qiskit.circuit.library import ZGate
 
 
def reflect(n: int) -> QuantumCircuit:
    qc = QuantumCircuit(n)
 
    qc.x(range(n))
    qc.append(ZGate().control(n - 1), range(n))
    qc.x(range(n))
 
    return qc
 
 
def solve(n: int, o: QuantumCircuit) -> QuantumCircuit:
    qc = QuantumCircuit(n)
 
    qc.h(range(n))
    qc.compose(o, inplace=True)
    qc.h(range(n))
    qc.compose(reflect(n), inplace=True)
    qc.h(range(n))
 
    return qc

B6: Grover's Algorithm I

解説

解答例