LogoQCoder Programming Contest 003
ログイン
← 前の解説次の解説 →

B5: Reflection Operator II

実行時間制限：3 秒

メモリ制限：512 MiB

配点：200点

Writer:Not_Leonian

解説

すべての量子ビットに HH ゲートを作用させると、ゼロ状態 ∣0⟩\ket{0} は ∣ψ⟩\ket{\psi} に遷移することに注目します。すなわち、∣ψ⟩\ket{\psi}は、

∣ψ⟩=H⊗n∣0⟩\begin{equation} \ket{\psi} = H^{\otimes n} \ket{0} \end{equation}

と表現できます。 また、 HH ゲートの性質から

H⊗n=(H⊗n)†, (H⊗n)2=I\begin{equation} H^{\otimes n}=(H^{\otimes n})^{\dagger},\ (H^{\otimes n})^2=I \end{equation}

が成立することと、随伴行列の性質から

⟨ψ∣=∣ψ⟩†=(H⊗n∣0⟩)†=∣0⟩†(H⊗n)†=⟨0∣H⊗n\begin{equation} \bra{\psi} = \ket{\psi}^{\dagger} = (H^{\otimes n} \ket{0})^{\dagger} = \ket{0}^{\dagger}(H^{\otimes n})^{\dagger} = \bra{0} H^{\otimes n} \end{equation}

が成立することを利用すると、2∣ψ⟩⟨ψ∣−I2 \ket{\psi}\bra{\psi} - I は以下のように変形できます。

2∣ψ⟩⟨ψ∣−I=2H⊗n∣0⟩⟨0∣H⊗n−(H⊗n)2=H⊗n(2∣0⟩⟨0∣−I)H⊗n\begin{equation} 2 \ket{\psi}\bra{\psi} - I = 2 H^{\otimes n} \ket{0}\bra{0} H^{\otimes n} - (H^{\otimes n})^2 = H^{\otimes n} (2 \ket{0}\bra{0} - I) H^{\otimes n} \end{equation}

よって、全ての量子ビットに HH ゲートを作用させてから、B4の回路を実装し、再度全ての量子ビットに HH ゲートを作用させることでこの問題を解くことができます。

n=3n = 3 の場合の回路図は、以下の通りです。回路図内のReflect_B4は、B4の回路を示しています。

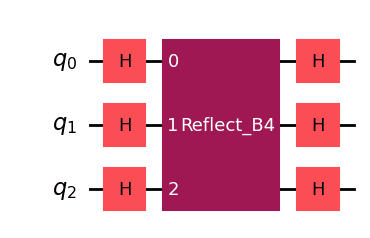
解答例

解答例は以下の通りです。

from qiskit import QuantumCircuit
from qiskit.circuit.library import ZGate
 
 
def reflect(n: int) -> QuantumCircuit:
    qc = QuantumCircuit(n)
 
    qc.x(range(n))
    qc.append(ZGate().control(n - 1), range(n))
    qc.x(range(n))
 
    return qc
 
 
def solve(n: int) -> QuantumCircuit:
    qc = QuantumCircuit(n)
 
    qc.h(range(n))
    qc.compose(reflect(n), inplace=True)
    qc.h(range(n))
 
    return qc