B2: Phase Shift Oracle

解説

計算基底状態 $\ket{L}$ のみに位相シフトゲート $P(\theta)$ を作用させる量子回路を実装する問題です。

では、重ね合わせ状態の中の特定の計算基底状態 $\ket{L}$ にのみ位相シフトゲート $P(\theta)$ を作用させるにはどうすればよいでしょうか？

これは次のように実現できます。

1. $\ket{L} = \ket{L_0 L_1 L_2 ... L_{n-1}}$ のうち、$L_i = 0$ であるようなインデックス $i$ に対して、$X$ ゲートを作用させる。こうして、$\ket{L}$ を $\ket{2^n - 1} = \ket{1...1}$ に変換する。
2. $n - 1$ ビットを制御ビット、残りの $1$ ビットを標的ビットとする複数制御位相シフトゲートを作用させる。このとき、位相シフトゲートは重ね合わせ状態の中の計算基底状態 $\ket{L}$ にのみ作用します。
3. 1. の逆操作を行い、$\ket{2^n - 1}$ を $\ket{L}$ に戻す。

この操作を実装することでこの問題を解くことができます。

$n = 3,\ L = 1$ の場合の量子回路は次のように表されます。

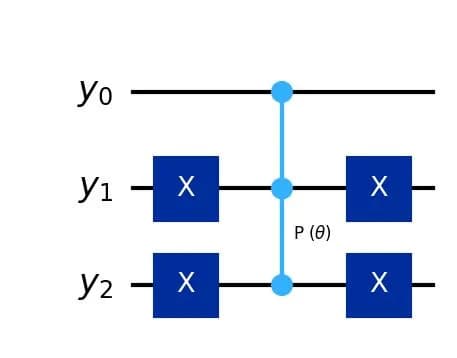
回路の深さは $3$ です。

解答例

解答例は以下の通りです。

from qiskit import QuantumCircuit
 
 
def solve(n: int, L: int, theta: float) -> QuantumCircuit:
    qc = QuantumCircuit(n)
 
    for i in range(n):
        if not (1 << i) & L:
            qc.x(i)
 
    if n == 1:
        qc.p(theta, n - 1)
    else:
        qc.mcp(theta, list(range(n - 1)), n - 1)
 
    for i in range(n):
        if not (1 << i) & L:
            qc.x(i)
 
    return qc