LogoQCoder Programming Contest 002
ログイン
← 前の解説次の解説 →

B1: Generate State eiθ∣0⟩e^{i\theta}\ket{0}

実行時間制限：3 秒

メモリ制限：512 MiB

配点：100点

Writer：PSL

解説ページではブラケット記法による解説を示しますが、B 問題はストリング図（ブラケット記法を発展させた二次元言語）による解説も提供されています。 ストリング図による Writer 解説 (pdf) を参照して下さい。

解説

今回の問題では、量子ゲートの一種である XX ゲートと 位相シフトゲート P(θ)P(\theta) を量子ビットに作用させることで、ゼロ状態 ∣0⟩\ket{0} から目的の量子状態 eiθ∣0⟩e^{i\theta}\ket{0} への遷移を実現できます。 以下の量子回路にて、行なったゲート操作を示します。

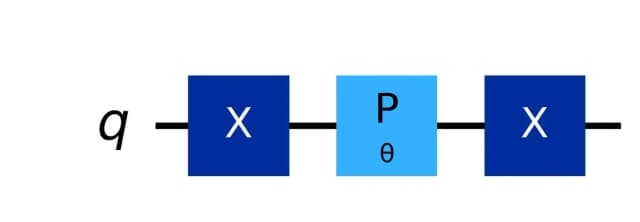
まず、 XX ゲートを量子状態 ∣0⟩\ket{0} に対して作用させることにより、量子状態 ∣1⟩\ket{1} へと遷移させます。

∣0⟩→X(0)∣1⟩\begin{equation} \ket{0} \xrightarrow{X(0)} \ket{1} \end{equation}

次に、位相シフトゲートを量子状態 ∣1⟩\ket{1} に対して作用させることにより、量子状態 eiθ∣1⟩e^{i\theta}\ket{1} へと遷移させます。

∣1⟩→P(θ,0)eiθ∣1⟩\begin{equation} \ket{1} \xrightarrow{P(\theta, 0)} e^{i\theta}\ket{1} \end{equation}

最後に、 XX ゲートを量子状態 −∣1⟩ - \ket{1} に対して作用させることにより、量子状態 −∣0⟩ - \ket{0} へと遷移させます。

eiθ∣1⟩→X(0)eiθ∣0⟩\begin{equation} e^{i\theta}\ket{1}\xrightarrow{X(0)} e^{i\theta}\ket{0} \end{equation}

eiπ∣0⟩=−∣0⟩e^{i\pi}\ket{0} = -\ket{0} より、本問は問題 A1 (Generate State −∣0⟩-\ket{0}) の一般化と考えることができます。

解答例

解答例は以下の通りです。

from qiskit import QuantumCircuit
 
 
def solve(theta: float) -> QuantumCircuit:
    qc = QuantumCircuit(1)
 
    qc.x(0)
    qc.p(theta, 0)
    qc.x(0)
 
    return qc