QCoder

解説

ビットがどのように変化するかを考えるのではなく、振幅がどのように変化するかを考えてみましょう。

$n=3, a=2, L=7$ の例を考えます。

基底状態 $\ket{i}$ の振幅を $A_i \neq 0$ とし、左から順に書くと、本問の遷移は以下のように表現できます。

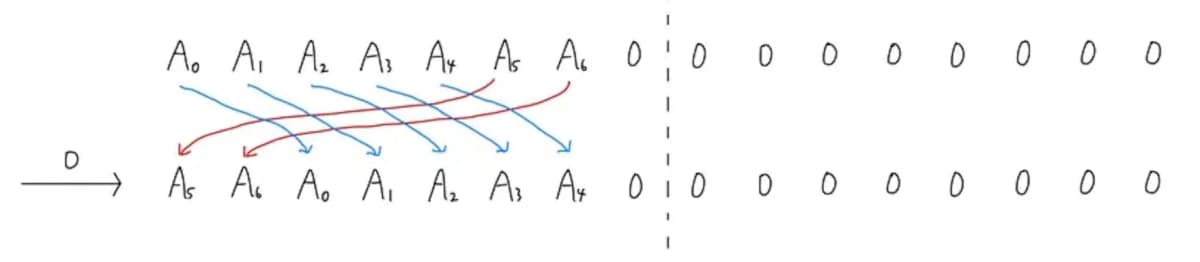
$A_{5}, A_{6}$ の2つは $A_{0}, A_{1}, A_{2}, A_{3}, A_{4}$ と異なる動きをしていることがわかります。

このとき、問題 B4 の操作で $s$ と $t$ を上手く選ぶと次のような遷移が実現できます。

よって、この問題の操作は次のようにして実現できます。

ただし、 $\mathrm{add}(a)$ は加算操作 $\ket{x} \rightarrow \ket{(x + a) \bmod 2^{n+1}}$ を表し、B3と同様に実装できます。

回路の深さは $O(n)$ です。

解答例

解答例は以下の通りです。

import math
 
from qiskit import QuantumCircuit
 
 
def qft(n: int) -> QuantumCircuit:
    qc = QuantumCircuit(n)
 
    for i in reversed(range(n)):
        qc.h(i)
        for j in reversed(range(i)):
            qc.cp(math.pi / 2 ** (i - j), j, i)
 
    for i in range(n // 2):
        qc.swap(i, n - i - 1)
 
    return qc
 
 
def crot(n: int, a: int) -> QuantumCircuit:
    qc = QuantumCircuit(n + 1)
 
    for i in range(n):
        theta = 2 * math.pi * a * 2**i / 2**n
        qc.cp(theta, n, i)
 
    return qc
 
 
def cadd(n: int, a: int) -> QuantumCircuit:
    qc = QuantumCircuit(n + 1)
 
    qc.compose(qft(n), qubits=range(n), inplace=True)
    qc.compose(crot(n, a), qubits=range(n + 1), inplace=True)
    qc.compose(qft(n).inverse(), qubits=range(n), inplace=True)
 
    return qc
 
 
# B4
def pack(n: int, s: int, t: int) -> QuantumCircuit:
    qc = QuantumCircuit(n + 1)
 
    qc.compose(cadd(n, 2 ** (n + 1) - t), qubits=range(n + 1), inplace=True)
    qc.x(n)
    qc.compose(cadd(n, -s), qubits=range(n + 1), inplace=True)
    qc.x(n)
 
    return qc
 
 
def rot(n: int, a: int) -> QuantumCircuit:
    qc = QuantumCircuit(n)
 
    for i in range(n):
        theta = 2 * math.pi * a * 2**i / 2**n
        qc.p(theta, i)
 
    return qc
 
 
def add(n: int, a: int) -> QuantumCircuit:
    qc = QuantumCircuit(n)
 
    qc.compose(qft(n), qubits=range(n), inplace=True)
    qc.compose(rot(n, a), qubits=range(n), inplace=True)
    qc.compose(qft(n).inverse(), qubits=range(n), inplace=True)
 
    return qc
 
 
def solve(n: int, a: int, L: int) -> QuantumCircuit:
    qc = QuantumCircuit(n + 1)
 
    qc.compose(add(n + 1, 2**n - L + a), qubits=range(n + 1), inplace=True)
    qc.compose(pack(n, 2**n - L + a, 2**n + a), qubits=range(n + 1), inplace=True)
    qc.compose(add(n + 1, a), qubits=range(n + 1), inplace=True)
 
    return qc

B5: Modular Arithmetic I

解説

解答例