LogoQCoder Programming Contest 004
ログイン
← 前の解説次の解説 →

A5: Minus One Oracle

実行時間制限：3 秒

メモリ制限：512 MiB

配点：300点

Writer：fortoobye

解説

はじめに、∣x⟩→∣(x−1) mod 2n⟩\ket{x} \rightarrow \ket{(x - 1) \bmod {2^n}} の逆操作である ∣x⟩→∣(x+1) mod 2n⟩\ket{x} \rightarrow \ket{(x + 1) \bmod {2^n}} という操作について考えます。

あらかじめ、xx を長さ nn のビット列 x0x1⋯xn−1x_0x_1 \cdots x_{n-1} を用いて表現することとします。

∣x⟩=∣x0x1⋯xn−1⟩n\begin{equation} \ket{x} = \ket{x_0x_1 \cdots x_{n-1}}_n \end{equation}

この表現を元に、∣x⟩→∣(x+1) mod 2n⟩\ket{x} \rightarrow \ket{(x + 1) \bmod {2^n}} という操作は以下のように言い換えることができます。

  • 下位ビットから順に 11 が連続する部分を全て 00 に変換し、はじめて 00 が出てくるビットを 11 に反転させる。
    • 具体的には、「 x0=x1=⋯=xi−1=1,xi=0x_0 = x_1 = \cdots = x_{i-1} = 1, x_{i} = 0 」となる ii (1≤i<n)(1 \leq i < n) を探し、x0,x1,⋯ ,xi−1x_0, x_1, \cdots , x_{i-1} を 00 に反転させ、xix_i を 11 に反転させます。 ただし、「 x0=x1=⋯=xn−1=1x_0 = x_1 = \cdots = x_{n-1} = 1 」となる時は、x0,x1,⋯ ,xn−1x_0, x_1, \cdots , x_{n-1} を 00 に反転させ、「 x0=x1=⋯=xn−1=0x_0 = x_1 = \cdots = x_{n-1} = 0 」となる時は、x0x_0 を 11 に反転させます。

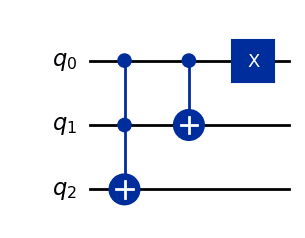
以下の n=3n = 3 の例をみてみましょう。

ここで、入力状態として ∣110⟩\ket{110} が与えられたとします。

まず、「1,21, 2 番目の量子ビットを制御ビット、33 番目の量子ビットを標的ビットとする複数制御 XX ゲート1」によって、以下の状態遷移が成り立ちます。

∣110⟩→MCX((0,1),2)∣111⟩\begin{equation} \ket{110} \xrightarrow{MCX((0,1),2)} \ket{111} \end{equation}

次に、「11 番目の量子ビットを制御ビット、22 番目の量子ビットを標的ビットとする制御 XX ゲート」によって、以下の状態遷移が成り立ちます。

∣111⟩→CX(0,1)∣101⟩\begin{equation} \ket{111} \xrightarrow{CX(0,1)} \ket{101} \end{equation}

最後に、XX ゲートによって、以下の状態遷移が成り立ちます。

∣101⟩→X(0)∣001⟩\begin{equation} \ket{101} \xrightarrow{X(0)} \ket{001} \end{equation}

結果として、∣110⟩→∣001⟩\ket{110} \rightarrow \ket{001} という操作を実現できていることが確認できます。

以上の操作を一般化すると、∣x⟩→∣(x+1) mod 2n⟩\ket{x} \rightarrow \ket{(x + 1) \bmod {2^n}} という操作を実現することができ、コードとしては以下のようになります。

from qiskit import QuantumCircuit
 
 
def solve(n: int) -> QuantumCircuit:
    qc = QuantumCircuit(n)
 
    for i in reversed(range(1, n)):
        qc.mcx(list(range(i)), i)
 
    qc.x(0)
 
    return qc

そして、それらのゲートを逆順に適用していくことで ∣x⟩→∣(x−1) mod 2n⟩\ket{x} \rightarrow \ket{(x - 1) \bmod {2^n}} という操作を実現できるため、結果としてこの問題を解くことができます。

解答例

解答例は以下の通りです。

from qiskit import QuantumCircuit
 
 
def solve(n: int) -> QuantumCircuit:
    qc = QuantumCircuit(n)
 
    qc.x(0)
 
    for i in range(1, n):
        qc.mcx(list(range(i)), i)
 
    return qc

次のように、∣x⟩→∣(x+1) mod 2n⟩\ket{x} \rightarrow \ket{(x + 1) \bmod {2^n}} に対して inverse メソッドを使って記述することもできます。

from qiskit import QuantumCircuit
 
 
def solve(n: int) -> QuantumCircuit:
    qc = QuantumCircuit(n)
 
    for i in reversed(range(1, n)):
        qc.mcx(list(range(i)), i)
 
    qc.x(0)
 
    return qc.inverse()

発展

整数 aa を 20,21,…2^0, 2^1, \ldots と 2n−20,2n−21,…2^n-2^0, 2^{n}-2^1, \ldots の和に分解すると、∣x⟩→∣x+a(mod2n)⟩\ket{x} \rightarrow \ket{x + a \pmod {2^n}} は本問題のアルゴリズムを高々 ⌈log⁡2(a)+12⌉\left\lceil \frac{\log_2(a) + 1}{2}\right\rceil 回適用して実現できます。

Footnotes

  1. Qiskit では複数制御ゲートを各ゲートクラスのもつ control メソッドを使って実装できます。 ↩