QCoder

解説

本問では次の状態遷移を実現するオラクル $O$ を実装します。

\begin{equation} \ket{x}_n \xrightarrow{O} \exp{\left(\frac{2\pi i f(x)}{2^m}\right)}\ket{x}_n \end{equation}

遷移後の状態は次のように各量子ビットごとに独立に分解できます。

\begin{align} \exp{\left(\frac{2\pi i f(x)}{2^m}\right)}\ket{x}_n &= \exp{\left(\frac{2\pi i ( S_0 x_0 + \cdots + S_{n-1}x_{n-1})}{2^m}\right)} \ket{x_0 \cdots x_{n-1}} \nonumber\\ &= \exp{\left(\frac{2\pi i S_0 x_0}{2^m}\right)} \ket{x_0} \otimes \exp{\left(\frac{2\pi i S_1 x_1}{2^m}\right)} \ket{x_1} \otimes \cdots \otimes \exp{\left(\frac{2\pi i S_{n-1} x_{n-1}}{2^m}\right)} \ket{x_{n-1}} \end{align}

よって、各量子ビット $x_i$ に対して $\theta = 2\pi S_i / 2^m$ の位相シフトゲートを作用させることでこの問題を解くことができます。

$n = 3$ の回路図を次に示します。

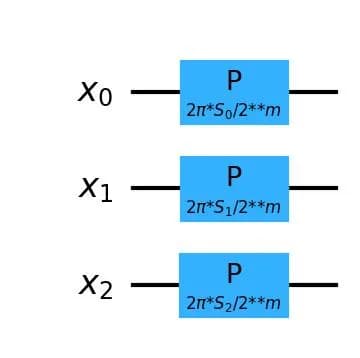
回路の深さは $1$ です。

解答例

解答例は以下の通りです。

import math
 
from qiskit import QuantumCircuit
 
 
def solve(n: int, m: int, S: list[int]) -> QuantumCircuit:
    qc = QuantumCircuit(n)
 
    for i in range(n):
        theta = 2 * math.pi * S[i] / 2**m
        qc.p(theta, i)
 
    return qc

B5: Quantum Arithmetic I

解説

解答例