解説
量子コンピュータでは「量子ゲート」という概念を用いて、量子ビットの状態を操作します。
今回の問題では、量子ゲートの一種である ゲートと ゲートを量子ビットに作用させることで、ゼロ状態 から目的の量子状態 への遷移を実現できます。 以下の量子回路にて、行なったゲート操作を示します。
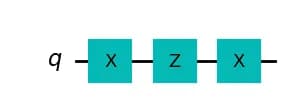
まず、 ゲートを量子状態 に対して作用させることにより、量子状態 へと遷移させます。
次に、 ゲートを量子状態 に対して作用させることにより、量子状態 へと遷移させます。
最後に、 ゲートを量子状態 に対して作用させることにより、量子状態 へと遷移させます。
この量子ビットを測定すると、元の状態と変わらず計算基底状態 が確率 で観測されます。一方で、 の グローバル位相 は から に変化しています。
このようなビット反転や位相反転は、基本の量子操作となります。
解答例
解答例は以下の通りです。
from qiskit import QuantumCircuit
def solve() -> QuantumCircuit:
qc = QuantumCircuit(1)
# Apply PauliX gate and PauliZ gate to the 1st qubit (index 0)
qc.x(0)
qc.z(0)
qc.x(0)
return qc補足
- Xゲート、Zゲート以外にも多くの量子ゲートが存在します。
それぞれの量子ゲートの意味や役割を理解しておくと、今後の問題を解く際に役立つかもしれません。